본 포스트는 저자가 학습하며 작성한 글 이기 때문에 틀린 내용이 있을 수 있습니다. 지적은 언제나 환영입니다.
1. 이진 탐색 (Binary Search)
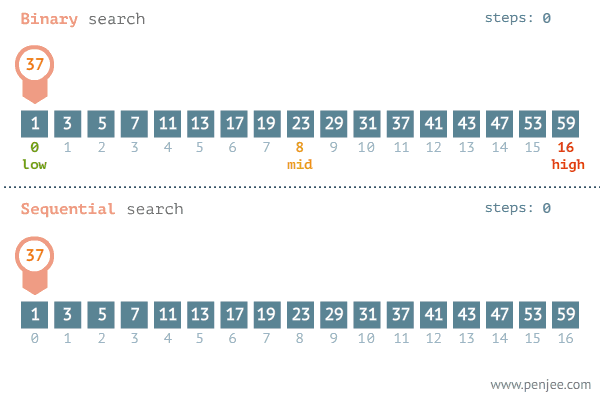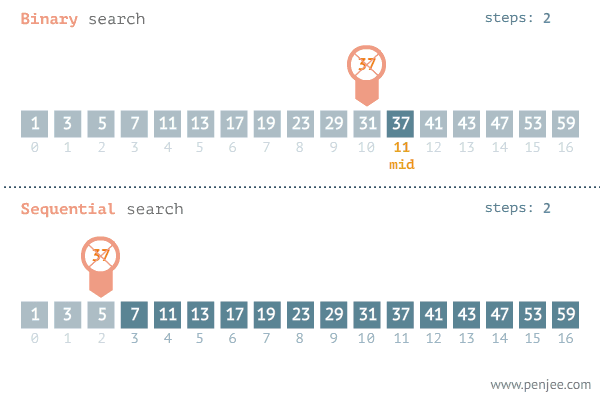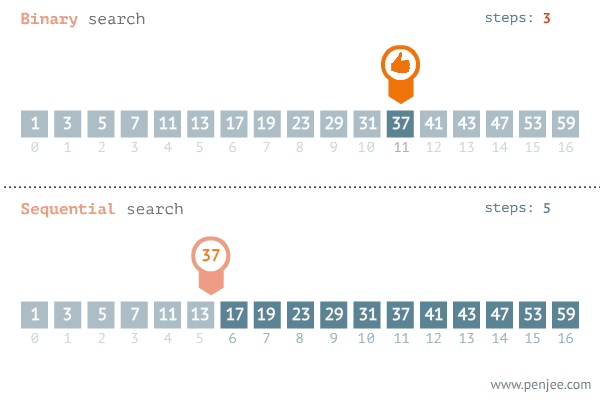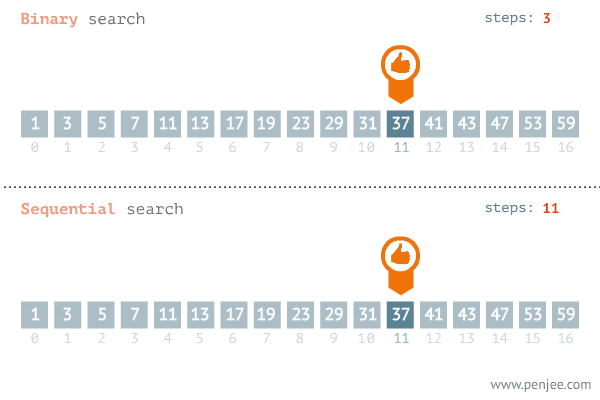
이진 탐색 (Binary Search) 은 정렬 되어 있는 리스트 에서 특정 값을 찾아내는 알고리즘이다. 오름차순, 내림차순의 여부는 크게 상관없으나 보통의 경우 '오름차순으로 정렬된 데이터' 를 사용한다. (정렬의 방향에 따라 탐색 범위를 좁혀가는 방향이 다르다)
탐색할 리스트의 중앙에 위치한 임의의 값을 선택하고 목표 값 (Target) 과 비교하여 탐색 범위를 좁혀간다.
만약 목표 값이 중앙 값보다 작다면 탐색 범위를 중앙 값 보다 작은 값들로 (좌측으로) 좁히고, 중앙 값 보다 크다면 탐색범위를 중앙 값 보다 큰 값들로 (우측으로) 좁힌다. 이를 더이상 탐색할 수 없을 때 까지 반복한다.
탐색 중 임의의 중앙 값이 목표 값과 일치한다면 탐색 성공이며, 탐색 끝까지 목표 값을 찾지 못하면 탐색 실패이다.
2. 시간 복잡도
흔히, 이진 탐색을 선형 탐색 (Linear Search) 와 비교한다. 선형 탐색은 리스트를 처음부터 끝까지 목표 값과 일일히 대조하며 탐색하는 방법이다. 장점이라 하면 정렬되지 않은 데이터도 탐색할 수 있지만, 처음부터 끝까지 탐색한다는 특징으로 인해 의 시간 복잡도를 갖는다.
이진 탐색은 한번의 탐색마다 탐색 범위가 절반으로 줄어드는 특징으로 인해 의 시간 복잡도를 '보장' 한다.
3. 구현
이진 탐색의 구현에서 동적 계획법 (Dynamic Programming) 과 재귀 (Recursion) 의 원리를 함께 알아볼 수 있다.
3-1. 재귀를 사용한 구현
def binary_search(data, target, low, high):
middle_idx = (high + low) // 2
middle = data[middle_idx]
if low > high: # 탐색 실패
return -1
if target == middle: # 탐색 성공
return middle_idx
elif target < middle:
return binary_search(data, target, low, middle_idx - 1)
elif target > middle:
return binary_search(data, target, middle_idx + 1, high)
data = [7,2,54,352,975,32,570,21]
sorted_data = sorted(data)
binary_search(sorted_data, 21, 0, len(data) - 1) # 2탐색 실패 즉, 주어진 data 안에 target 이 존재하지 않을 경우 언젠가 low 가 high 보다 커지게된다. 그렇지 않고 target == middle 인 경우 탐색 성공이다.
3-1. 재귀를 사용하지 않은 구현
def binary_search(data, target, low, high):
while low <= high:
middle_idx = (low + high) // 2
middle = data[middle_idx]
if middle == target:
return middle_idx
elif target < middle:
high = middle_idx - 1
elif target > middle:
low = middle_idx + 1
return -1
data = [7,2,54,352,975,32,570,21]
sorted_data = sorted(data)
binary_search(sorted_data, 21, 0, len(data) - 1) # 24. 정리
- 정렬된 데이터에서 목표 값을 찾는 알고리즘
- 한번 탐색할 때 마다 탐색 데이터 개수는 절반이 됨
- 따라서 의 시간복잡도를 갖음