본 포스트는 Do it! 자료구조와 함께 배우는 알고리즘 입문 : 파이썬 편의 일부를 참고하여 작성하였습니다.
본 포스트는 저자가 학습하며 작성한 글 이기 때문에 틀린 내용이 있을 수 있습니다. 지적은 언제나 환영입니다.
1. 개요
1-1. 해시 테이블
해시 테이블 (또는 해시 맵 이라고도 한다) 은 1950년대에 등장했지만, 아직도 많은 곳에서 유용하게 사용되는 자료구조이다. 해시테이블은 데이터를 Key-Value 쌍으로 저장하는 자료구조이다. 대표적으로 Python 의 딕셔너리가 해시 테이블로 구현되어 있다.
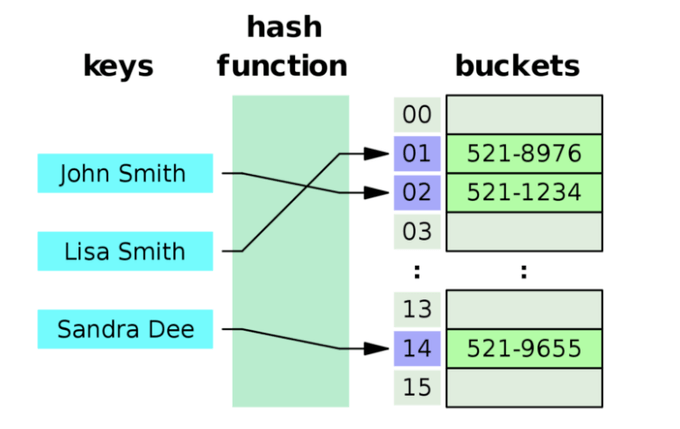
해시 테이블은 Key 를 받아 임의의 해시 함수를 통해 도출된 해시 값을 배열의 Index 로 사용한다. 이런 방식을 통해 O(1) 이라는 아주 빠른 속도로 데이터에 접근할 수 있다. 하지만, Index 가 순서대로 사용되어 차곡차곡 데이터가 적재되지 않아 빈 공간이 생기고, 이는 공간의 낭비로 이어진다. 즉, 해시 테이블은 공간과 시간이 Trade-Off 의 관계에 있다. 공간으로 시간을 사는 개념이라고 보면 좋다.
해시 테이블의 배열의 각 원소를 버킷 (Bucket) 이라고 한다. 버킷의 개수는 고정적이다. 후술할 해시 충돌 을 해결하기 위해 각 버킷에는 링크드 리스트 등을 사용하여 여러 데이터를 저장하게 되는데, 이를 슬롯 (Slot) 이라고 한다. 한 버킷에는 여러개의 슬롯이 저장될 수 있으며, 슬롯의 개수는 가변적이다. 쉽게 생각하면 버킷은 행, 슬롯은 열 이라고 봐도 괜찮다.
1-2. 해시 함수
해시함수란 임의 길의의 데이터를 고정 길이의 데이터로 매핑하는 함수이다. 간단하게는 13 으로 나눈뒤 나머지를 구하는 함수도 해시함수라고 할 수 있다. 이런 해시함수를 사용하면 발생하는 문제가 한가지 존재하는데, 예를 들어 Key 값을 13 으로 나눈 나머지를 Index 로 사용하는 해시 테이블이 있다고 가정해보자. 또한 이 해시 테이블에는 현재 Key 가 5인 값이 들어가 있는 상황이다.
이 해시 테이블에 Key 가 18 인 데이터를 저장하려 해보자. 하지만, 18 의 해시 값도 5, 즉 Index 가 중복되기 때문에 충돌 (Collision) 이 발생한다.
해시함수는 1:1 관계가 아닌, 1:N 관계이기 때문에 발생하는 문제이다. 해시함수는 서로 다른 두 값을 해싱 했을 때, 무조건 다른 해시 값이 도출됨을 보장하지 않는다. 즉, 중복이 발생할 수 있다는 것이다.
해시 함수는 연산이 빠르고, 충돌이 적고, 고르게 분포될 수록 좋은 함수라고 평가 받는다.
1-3. 해시 충돌 대응
충돌을 대응하는 방식에는 아래와 같이 크게 두가지 방법이 있다.
-
Chaining
각 버킷에 대응하는 링크드 리스트를 생성하고, 버킷이 링크드 리스트의 가장 앞 노드를 바라보게끔 하여 충돌을 방지하는 방법이다. 해시 충돌이 발생했을 때 그저 같은 버킷 링크드 리스트의 마지막 노드로 해당 값을 추가해주기만 하면 된다. 열린 해시법이라고도 한다.
-
Open addressing
Chaining 방법과 다르게 한 버킷에는 하나의 Value 만 저장하며, 해시 충돌 시 Key 를 재해싱(rehasing) 하여 빈 버킷에 데이터를 저장하는 방법이다. 닫힌 해시법이라고도 한다.
2. Chaining 방식 구현하기
이번엔 파이썬으로 직접 해시 테이블을 구현해보자. 사실 파이썬은 이미 딕셔너리라는 훌륭한 해시 테이블을 내장하고 있지만, 실 사용보다는 원리를 알아보는데에 목적이 있으므로 넘어가도록 한다.
첫번째로 구현할 방식은 Chaining 방식이다.
2-1. Hash 값 구하기
파이썬에서 해시 테이블에서 사용되는 Key 값을 Hasing 하는 방법에는 여러가지가 있을 수 있다. 본 포스트에서는 해시 테이블의 크기로 나눈 값의 나머지로 Index 를 구할 것 이다. 하지만, Key 값이 꼭 정수형으로 들어온다는 보장은 없다. 따라서 sha256 을 이용하여 정수형이 아닌 데이터도 Hashing 하여 우리의 Index 규칙에 맞게 바꿔줄 것 이다.
import hashlib
HASH_TABLE_SIZE = 13
def hash_value(key):
if isinstance(key, int): # 만약 key 값이 정수형이라면
return key % HASH_TABLE_SIZE # 해시테이블 크기로 나눈 나머지를 반환
# 정수형이 아닌 값의 해싱
return int(hashlib.sha256(str(key).encode()).hexdigest(), 16) % HASH_TABLE_SIZE정수형이 아닌 Key 값은 str(key).encode() 를 통해 Byte 로 변환해주고, hashlib.sha256(...).hexdigest() 을 통해 해당 값을 sha256 으로 Hashing 한 뒤 16진수인 Digest 값을 가져온다. 그 다음 int(..., 16) 를 통해 16진수를 10진수로 바꿔준 다음 % HASH_TABLE_SIZE 연산을 해준다.
해시 함수를 통해 나온 결과값을 해쉬 값 혹은 다이제스트 (Digest) 라고 한다.
이 때, 해시 테이블의 크기로 나눈 나머지 값을 Index 로 사용하는 이유는 최대 Index 를 해시테이블 크기에 딱 맞게 계산할 수 있기 때문이다.
2-2. Node 클래스 정의
Chaining 방식으로 구현을 할 것이므로 각 버킷에 대응하는 링크드 리스트를 구현해야한다. 링크드 리스트의 각 노드를 담당하는 Class 를 우선으로 구현하자.
class Node:
def __init__(self, key, value, next):
self.key = key
self.value = value
self.next = nextkey 와 value 그리고 다음 노드를 가리키는 next 를 멤버변수로 하는 Node 클래스를 정의해주었다.
2-3. ChainedHash 클래스 정의
class ChainedHash:
def __init__(self, size):
self.size = size
self.table = [None] * self.size
def hash_value(self, key):
if isinstance(key, int):
return key % self.size
return int(hashlib.sha256(str(key).encode()).hexdigest(), 16) % self.size해시 테이블의 크기인 size 와 버킷으로 사용될 table 을 멤버 변수로 갖는 ChainedHash 클래스를 정의하였다. 그리고 위에서 미리 만들어둔 hash_value 함수를 메소드로 넣어주었다.
hashlib 이 import 되어있어야 한다.
2-4. add (추가) 메소드 정의
def add(self, key, value):
hash = self.hash_value(key)
pointer = self.table[hash]
while pointer != None:
if pointer.key == key:
return False
pointer = pointer.next
self.table[hash] = Node(key, value, self.table[hash])
return Truekey 를 파라미터로 받아와 해싱한다. 그 해시 값을 Index 로 버킷에 접근한다. 포인터 변수를 하나 두고, 원하는 key 에 해당하는 노드를 찾을 때 까지 탐색한다. 노드를 찾으면 이미 중복된 키가 존재하는 경우이므로 삭제 실패, False 를 반환한다. 노드를 찾지 못한 경우 키가 중복되지 않으므로 self.table 에 Index 로 접근해 나중에 추가된 노드가 링크드 리스트 가장 앞에 오도록 노드를 추가한다.
2-5. search (탐색) 메소드 정의
def search(self, key):
hash = self.hash_value(key)
pointer = self.table[hash]
while pointer != None:
if pointer.key == key:
return pointer.value
pointer = pointer.next
return Noneadd 메소드와 같은 방법으로 버킷을 찾고 버킷이 가리키는 링크드 리스트를 탐색하며 일치하는 키의 노드를 찾으면 그 노드의 value 를 반환한다. 찾지 못하면 None 을 반환한다.
2-6. remove (제거) 메소드 정의
def remove(self, key):
hash = self.hash_value(key)
pointer = self.table[hash]
# 버킷의 첫번째 노드와 주어진 Key 가 일치하면
if pointer.key == key:
# 해당 버킷을 None 으로 만듦
self.table[hash] = None
return True
# 버킷의 첫번째 노드와 주어진 Key 가 일치하지 않으면
else:
# 다음 노드가 None 일때까지 반복 (버킷의 마지막 노드의 직전 노드까지 반복)
while pointer.next != None:
# 다음 노드의 키가 주어진 key 와 일치하면 반복 탈출
# 즉 최종적으로 pointer 는 삭제 대상 노드의 전 노드를 가리킴
if pointer.next.key == key:
break
pointer = pointer.next
# 다음 노드가 None 인 경우는
# (1) 제거 대상이 버킷의 첫번째 노드 일때
# (2) 버킷의 모든 노드를 탐색하였지만 제거대상을 찾지 못했을 때
# 즉, 제거대상이 테이블에 존재하지 않을 때
# 아래 코드는 (2) 의 경우를 처리함
if pointer.next == None:
return False
# 가리키고 있는 노드의 다음 노드를 다다음 노드로 교체, 즉 삭제
pointer.next = pointer.next.next
return True줄글로 설명하기에 조금 복잡하여 주석으로 대체하였다. 사실상 링크드 리스트의 노드 삭제 방법과 일치한다.
3. Open Addressing 방식 구현하기
위에서 Open Addressing 방식은 해시 충돌이 발생하였을 때, 재해싱 한다고 하였다. 더 자세히 이야기 하자면, 충돌이 발생한 버킷의 다음 버킷을 탐색하고, 또 충돌한다면 그 다음 버킷을 탐사하는 과정을 반복하는 선형 탐사 (Linear Probing) 를 하는 방식이다.
Chaining 방식과 다르게 링크드 리스트와 같은 추가적인 메모리를 사용하지 않고, 빈 버킷을 탐색하여 데이터를 저장하는 방식이기 때문에 메모리를 덜 사용하게 되는 이점이 존재한다.
참고로 파이썬의 Dictionary 는 Open Addressing 방식을 채택했다고 한다.
3-1. 버킷 상태 열거형 클래스 정의
from enum import Enum
import hashlib
class Status(Enum):
OCCUPIED = 0
EMPTY = 1
DELETED = 2버킷의 상태는 크게 점유됨 (OCCUPIED), 비어있음 (EMPTY), 삭제됨 (DELETED) 으로 구분한다. 삭제됨 상태를 굳이 구분한 이유는 따로 있다.
데이터를 추가하는 중 3번째 버킷에서 충돌이 발생하여, 재해싱 후 4번째 버킷에 데이터를 등록한 상황을 가정해보자. 그리고 그 이후 3번째 버킷이 삭제되었다고 해보자. 이 때 DELETED 상태가 따로 정의되지 않은 상황이라면, 3번째 버킷에는 EMPTY 상태를 지정할 수 밖에 없다. 이런 경우 4번째 버킷을 검색할 때, 최초 해시값은 3번째 버킷과 일치할 텐데, 해당 버킷은 상태가 EMPTY 일테고 데이터가 없다고 판단되어 검색은 실패되고 종료될 것 이다.
즉, DELETED 상태는 '이 버킷은 비어있긴 한데, 해시 충돌로 재해싱되어 다른 버킷에 저장된 데이터가 있으니까 선형탐사해봐' 라고 전달하는 것과 동일하다.
3-2. Bucket 클래스 정의
class Bucket:
def __init__(self, key = None, value = None, stat = Status.EMPTY):
self.key = key
self.value = value
self.stat = stat
def set(self, key, value, stat):
self.key = key
self.value = value
self.stat = stat
def set_status(self, stat):
self.stat = stat해시 테이블의 각 원소로 사용될 Bucket 클래스를 정의한다. key , value 그리고 상태를 나타내는 stat 멤버 변수를 가지고 있으며, 필드 전체를 설정할 수 있는 set 메소드와 상태만을 설정하는 set_status 메소드가 정의되어 있다.
3-3. OpenHash 클래스 정의
class OpenHash:
def __init__(self, size):
self.size = size
self.table = [Bucket()] * self.size
def hash_value(self, key):
if isinstance(key, int):
return key % self.size
return int(hashlib.sha256(str(key).encode()).hexdigest(), 16) % self.sizeChaining 방식과 동일하게 해시 테이블의 길이인 size 와 각 원소가 저장될 배열 table 를 정의한다. 단, 이때 각 원소는 위에서 정의한 Bucket 클래스를 사용한다. 또한 똑같이 hash_value 메소드를 정의한다.
3-4. rehash_value (재해싱) 메소드 정의
위 OpenHash 클래스 hash_value 메소드 아래에 계속 이어 작성한다.
def rehash_value(self, key):
return (self.hash_value(key) + 1) % self.size재해싱하는 메소드 rehash_value 를 정의한다. 기존의 해시값에 1을 더해 다시 나머지 연산으로 해시하는 함수이다. 즉 한칸 오른쪽의 버킷을 가리키게 된다. 단, 기존의 해시값이 가장 마지막 버킷을 가리킨다면, 나머지 연산으로 인해 첫번째 버킷을 가리키게 된다.
3-5. search_node (노드 검색) 메소드 정의
def search_node(self, key):
hash = self.hash_value(key)
pointer = self.table[hash]
for i in range(self.size):
# 버킷이 비어있을 때는 None 반환
if pointer.stat == Status.EMPTY:
break
# 버킷이 할당되어있고, Key 까지 일치하면 지금 가리키고 있는 버킷 반환
elif pointer.stat == Status.OCCUPIED and pointer.key == key:
return pointer
# (1) 버킷이 할당되어 있으나 Key 가 일치하지 않을 떄
# (2) 지금 가리키고 있는 버킷은 삭제되었지만,
# 재해싱하여 다른 버킷에 저장된 데이터가 있을 때 (stat == DELETED)
hash = self.rehash_value(hash)
p = self.table[hash]
return None
def search(self, key):
pointer = self.search_node(key)
if pointer is not None:
return pointer.value
else:
return None테이블에서 버킷을 검색해 일치하는 버킷을 반환하는 search_node 메소드와, 일치하는 버킷의 value 를 반환하는 search 메소드를 정의한다.
search_node 메소드를 살펴보자. 일단, 버킷의 크기만큼 반복한다. 그리고 pointer 가 최초로 가리키는 버킷은 최초 해시값에 해당하는 버킷일 것 이다. 만약 그 버킷이 EMPTY 라면, 더 검색해볼 필요 없이 None 을 반환하면 된다. 그렇지 않고, 버킷이 점유되어 있으며 key 까지 일치한다면 검색에 성공하였으므로 해당하는 버킷을 반환한다.
만약 (1) 버킷이 할당되어 있지만 key 는 일치하지 않을때 (2) 지금 가리키고 있는 버킷은 삭제되었지만, 재해싱되어 다른 버킷에 데이터가 있는 경우 ( stat == Status.DELETED ) 일때는 재해싱하여 선형탐사를 해야한다. 이 때, 최대 버킷의 크기 - 1 번 선형탐사를 하게 되고, elif 절의 조건과 만족하게 되면 해당 버킷을 반환한다.
3-6. add (추가) 메소드 정의
def add(self, key, value):
# 이미 중복된 키가 존재
if self.search(key) is not None:
return False
hash = self.hash_value(key)
pointer = self.table[hash]
for i in range(self.size):
if pointer.stat == Status.EMPTY or pointer.stat == Status.DELETED:
self.table[hash] = Bucket(key, value, Status.OCCUPIED)
return True
hash = self.rehash_value(hash)
pointer = self.table[hash]
return False먼저 search 메소드로 이미 같은 key 를 가지고 있는 버킷이 있는지 검색한다. 중복된 key 가 없다면 추가를 진행한다.
추가할 때도 search_node 메소드와 마찬가지로 충돌 발생 시 (버킷이 EMPTY 혹은 DELETED 가 아닌 경우) 재해싱하여 비어있는 버킷에 값을 할당하는 작업을 진행한다. 만약 해시 테이블의 모든 원소에 추가 시도를 하였으나, 실패한 경우 버킷 용량이 부족한 것으로 판단되어 False 를 반환한다.
3-7. remove (삭제) 메소드 정의
def remove(self, key):
pointer = self.search_node(key)
# 등록되지 않은 키의 삭제는 실패
if pointer is None:
return False
pointer.set_status(Status.DELETED)
return Truesearch_node 메소드로 등록되지 않는 키 여부를 확인한 뒤, 등록된 키라면 해당 버킷의 상태를 DELETED 로 변경한다.
마치며
이렇게 파이썬에서 간단히 해시 테이블을 구현해보며 공부해보았다. Javascript 의 Object, Python 의 Dictionary 등 내장된 해시 테이블 자료구조가 어떻게 동작하는지 알고있지 않았는데, 이 기회에 좀 더 깊은 지식을 얻게 되어 즐거웠다 😊